Groundwater circulation in gypsiferous horizons and subsequent erosion is frequently the reason for geomechanical problems such as subsidence or even collapse. In order to provide a basis for reliable risk assessment, an adequate hydrogeological characterization of gypsum karst aquifers is required, mainly focusing on the geometric and hydraulic properties of the highly conductive conduit network. However this is not easily achieved by standard investigation techniques such as hydraulic tests. Therefore, Liedl & Sauter (1998) suggested an integrated modelling approach combining both long-term simulations of aquifer genesis and short-term simulations of transport phenomena in karst aquifers. MODELLING APPROACH A karst groundwater flow system may be conceptualized as a flow system consisting of a so-called fissured system, which represents the mass of the fractured rock, and a conduit system representing the karst pipe network. Groundwater flow in the fissured system is modelled using Boussinesq's equation. Flow in the conduit system is governed by Kirchhoff s law that states that the total inflow and total outflow balance Characterization of gypsum aquifers using a coupled contiuum-pipe flow model 17 for each node of the conduit network. For each pipe the discharge is related to the head difference by the Darcy-Weisbach equation which is adapted to laminar and turbulent flow conditions. Exchange of groundwater between the conduits and the fissured system is assumed to be proportional to the hydraulic head difference between these flow systems. Mass transport in the conduits is described by the one-dimensional (1-D) advection equation with an additional source term accounting for the increase in concentration due to the dissolution reaction. Clemens et al. (1996) implemented this modelling approach for carbonate aquifers in the CAVE (Carbonate Aquifer Void Evolution) code, which added conduit flow and limestone dissolution to the well-known MODFLOW code. To simulate the evolution of voids in gypsum aquifers for a variety of boundary conditions, EVE combines the updated MODFLOW-96 code (McDonald & Harbaugh, 1996) with the conduit flow module from CAVE and a newly developed evaporite dissolution module.
where δM/δt is the mass loss from the solid surface with the surface area A, h is the mass transfer coefficient, ceq is the equilibrium concentration, and c is the concentration in the bulk solution.
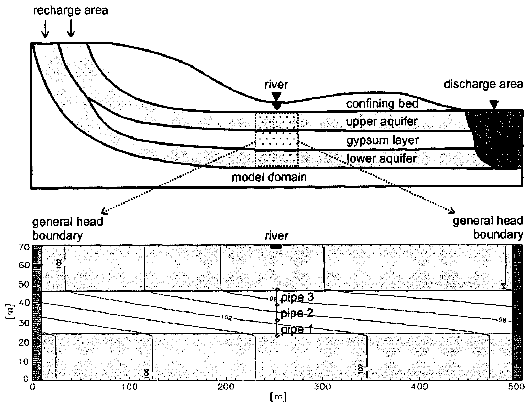
For laminar flow conditions, a fully developed diffusion boundary layer is assumed, i.e. Sh = 3.66 in circular pipes with a parabolic velocity profile, whereas the Sherwood number for turbulent flow conditions is given by an empirical correlation (Incropera & DeWitt, 1996). MODEL SCENARIO It is generally believed that the evolution of gypsum karst starts under artesian conditions (Klimchouk, 1996b), a typical setting consisting of two confined aquifers separated by a gypsum layer. The model domain studied in this paper consists of a two-dimensional (2-D) cross-section with a total thickness of 70 m subdivided into a gypsum layer of 22 m and two aquifers of 24 m thickness (Fig. 1). The general head boundaries represent a recharge area over a distance of 2 km at a level of 150 m, and a discharge area at a distance of 2 km at a level of 70 m. In addition, a river drains the upper aquifer with a leakage factor of 2 x 10-9 m-1 and a water level of 75 m. This setup imposes a hydraulic head gradient between the aquifers and causes an upward directed flow from the lower to the upper aquifer. The hydraulic conductivity is set to 10-6 for the aquifers and l0-9 m s-1 for the gypsum layer. A single conduit of 0.4 mm diameter intersects the gypsum layer. At four nodes, which subdivide the conduit into three pipes, an exchange of water between the conduit and the fissured system is allowed. Since flow is always from the lower aquifer into the gypsum layer, the gypsum concentration of water flowing in the lower aquifer is assumed to be zero. The water flowing in the gypsum layer is assumed to be saturated with respect to gypsum.
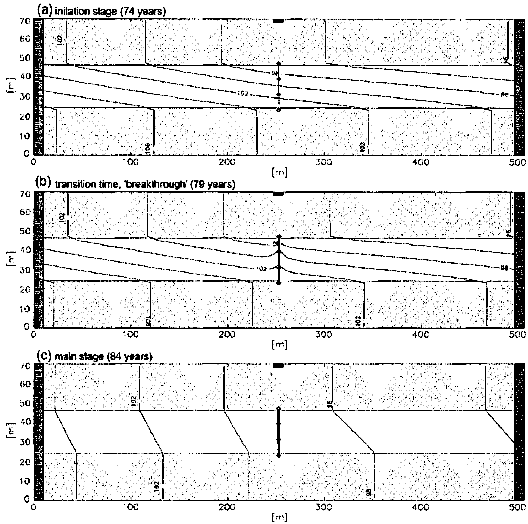
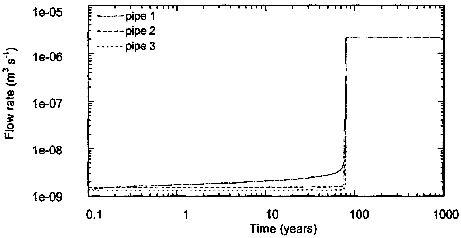
SIMULATION RESULTS Regarding pipe diameters and hydraulic heads, three stages of conduit development can be distinguished (Fig. 2). At the initiation stage the water flowing from the conduit into the upper aquifer is saturated with respect to gypsum. Therefore, the outlet of the conduit is not enlarged and restricts the discharge. Due to the sluggish flow conditions the conduit growth is very slow and the hydraulic head gradient between the aquifers is maintained (Fig. 2(a)). However, the inlet of the conduit is enlarged by the strongly undersaturated water entering the conduit. Thus, the hydraulic head of the lower aquifer propagates upward through the conduit, and the hydraulic head gradient along the upper part of the conduit (i.e. pipe 3) increases accordingly (Fig. 2(b)). As a result the discharge through the conduit increases, and eventually the water emerging at the outlet of the conduit is undersaturated with respect to gypsum. In this situation a positive feedback mechanism triggers a rapid conduit growth (breakthrough), since the Characterization of gypsum aquifers using a coupled contiuum-pipe flow model enlargement of the outlet due to gypsum dissolution results in increasing flow rates and decreasing concentrations and thus higher dissolution rates. Finally the hydraulic head gradient between the aquifers is diminished (Fig. 2(c)).
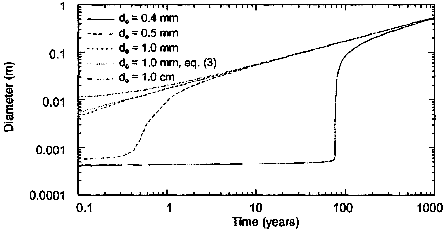
A further parameter, which is expected to be a controlling factor in conduit genesis, is the initial pipe diameter d0. Therefore, several model runs starting with different initial diameters were performed (Fig. 4). Although the breakthrough time is very sensitive to the initial diameter, the final diameter of the conduit (pipe 1) is nearly the same after 1000 years in each case. Thus, considering the long-term evolution, i.e. a period which is long relative to the breakthrough time, conduit development is insensitive to the initial diameter. Moreover, this long-term evolution can be described analytically by inserting equation (2) in equation (1) and setting δM(t) = ½pAδ(t), where p is the density of gypsum, and d(t) is the pipe diameter at time t. The resulting relationship can be solved for the pipe diameter yielding:
Figure 4 shows the temporal evolution of the diameter of pipe 1 comparing EVE results with the analytical solution given by equation (3). Since for the given model Characterization of gypsum aquifers using a coupled contiuum-pipe flow model 21 scenario the gypsum concentration after the breakthrough is very small compared with the equilibrium concentration, a concentration c = 0 was inserted in equation (3), and the function was plotted for an initial diameter of 1 mm. Smaller initial diameters result in the same straight line as for do = 1 mm, whilst the plot of equation (3) for an initial diameter of 1 cm yields the same result as calculated by EVE.
Equation (3) demonstrates that the influence of the initial diameter is negligible for long time periods. Conduit enlargement at the main stage is only controlled by the density of the rock, by the undersaturation of the water with respect to gypsum, and by parameters which describe the diffusion process of gypsum from the solid surface into the bulk solution (Sh and D). Note however that the concentration of gypsum in the water depends on the flow rate. CONCLUSIONS At the initiation stage, conduit development under artesian conditions is controlled by the initial diameter of the conduit and by the exchange of water between the conduit and the gypsum layer. However, at the late stage conduit growth is insensitive to these parameters. The long-term evolution of conduits with different initial diameters leads to similar diameters, which can be predicted by an analytical solution. Acknowledgements This work is part of the ROSES (Risk of Subsidence due to Evaporite Solution) project funded by the European Commission Framework IV Programme (Contract number ENV4-CT97-0603). REFERENCES
|